数据结构——栈

148次阅读

没有评论

共计 1764 个字符，预计需要花费 5 分钟才能阅读完成。

1、数组（Aarray）

2、栈（Stack）

3、链表（Linked List）

4、图（Graph）

5、散列表（Hash）

6、队列（Queue）

7、树（Tree）

8、堆（Heap）

数组是一个线性结构，并且可以在数组的任意位置插入和删除元素。而栈和队列就是比较常见的受限的线性结构。

先进后出，后进先出（LIFO：last in first out）

数据结构——栈

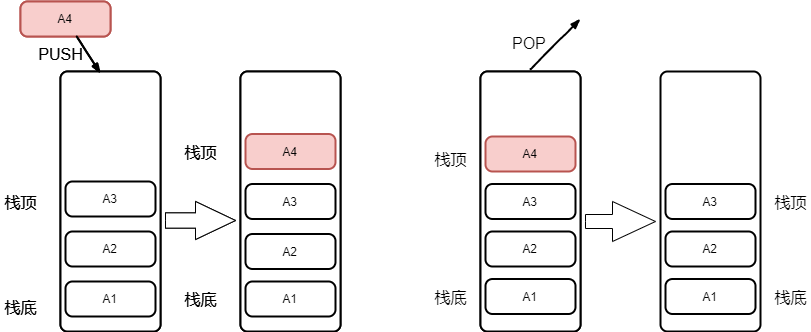
程序中的栈结构：

1、 函数调用栈：A（B（C（D（））））：即 A 函数中调用 B，B 调用 C，C 调用 D；在 A 执行的过程中会将 A 压入栈，随后 B 执行时 B 也被压入栈，函数 C 和 D 执行时也会被压入栈。所以当前栈的顺序为：A->B->C->D（栈顶）；函数 D 执行完之后，会弹出栈被释放，弹出栈的顺序为 D ->C->B->A;

2、递归：为什么没有停止条件的递归会造成栈溢出？比如函数 A 为递归函数，不断地调用自己（因为函数还没有执行完，不会把函数弹出栈），不停地把相同的函数 A 压入栈，最后造成栈溢出（Stack Overfloat）

1、push（element）：添加一个新元素到栈顶位置；

2、pop（）：移除栈顶的元素，同时返回被移除的元素；

3、peek（）：返回栈顶的元素，不对栈做任何修改（该方法不会移除栈顶的元素，仅仅返回它）；

4、isEmpty（）：如果栈里没有任何元素就返回 true，否则返回 false；

5、size（）：返回栈里的元素个数。这个方法和数组的 length 属性类似；

interface StackItem {value: number | string | Function;}
class Stack {protected items: StackItem[];

    constructor() {this.items = [];
    }

    public push(StackItem): void {this.items.push(StackItem);
    }

    public pop(): StackItem {return this.items.pop()
    }

    public peak(): StackItem {return this.items[this.items.length - 1]
    }

    public isEmpty(): boolean {return this.items.length == 0}

    public size(): number {return this.items.length}
}

let  stack: Stack = new Stack();
stack.push(1);
stack.push(2);
stack.push(3);
stack.push(4);
console.log(stack);            // Stack {items: [ 1, 2, 3, 4] }
console.log(stack.items);      // [1, 2, 3, 4]
console.log(stack.pop());      // 4
console.log(stack.peak());     // 3   栈顶 的值从 4 变为了 3
console.log(stack.pop());      // 3
console.log(stack.peak());     // 2   栈顶 的值从 3 变为了 2
console.log(stack.isEmpty());  // false
console.log(stack.size());     // 2

1．进栈（PUSH）算法
①若 TOP≥n 时，则给出溢出信息，作出错处理（进栈前首先检查栈是否已满，满则溢出；不满则作②）；
②置 TOP=TOP+1（栈指针加 1，指向进栈地址）；
③S(TOP)=X，结束（X 为新进栈的元素）；
2．退栈（POP）算法
①若 TOP≤0，则给出下溢信息，作出错处理 (退栈前先检查是否已为空栈，空则下溢；不空则作②)；
②X=S(TOP)，（退栈后的元素赋给 X）：
③TOP=TOP-1，结束（栈指针减 1，指向栈顶）。

	top 指向栈顶元素的下一个位置	top 指向栈顶元素
初始化	S.top=S.base	S.top=S.base-1
判断空	S.base==S.top	S.base==S.top-1
进栈	*S.top++=e	*++S.top=e
栈满	S.top-S.base>=S.stacksize	S.top-S.base>=S.stacksize-1
出栈	e=*–S.top	e=*S.top–